Bulter-Volmer方程与过电位

Butler-Volmer equation：

$$i=i_c-i_a=FAk^0 \left [c_O(0,t) \exp \dfrac{-\beta F(E-E^{0\prime})}{RT}- c_R(0,t) \exp \dfrac{(1-\beta)F(E-E^{0\prime})}{RT}\right] \tag {1}$$

Exchange current

$$i_0=FAk^0 c_O^{∗(1−β)}c_R^{∗β} \tag{2}$$

---

current-overpotential （$i-\eta$）equation

此处把标准电位$E^{0\prime}$的参考点替换为平衡电位$E_{eq}$,定义过电位Overpotential $\eta = E-E_{eq}$，(1)式可以写成电流与过电位的关系式$\eta-i$
在平衡电位$E_{eq}$，且在平衡状态时，氧化物，还原物各自的本体浓度与表面浓度相等，即$c_O=c_O^*$与$c_R=c_R^*$，由方程(1)可得

$$0=FAk^0 \left [c_O(0,t) \exp \dfrac{-\beta F(E-E^{0\prime})}{RT}- c_R(0,t) \exp \dfrac{(1-\beta)F(E-E^{0\prime})}{RT}\right] \tag {3}$$

得到

$$\exp \dfrac{ F(E_{eq}-E^{0\prime})}{RT}=\dfrac {c_O^*}{c_R^*} \tag{4}$$ $$i=FAk^0 \left [c_O(0,t) \exp \dfrac{-\beta F}{RT} \eta- c_R(0,t) \exp \dfrac{(1-\beta)F}{RT} \eta \right] \tag {5}$$

方程(5)与方程(2)互比得到

$$\dfrac {i}{i_0}=\dfrac{c_O(0,t)}{c_O^{*(1-\beta)} c_R^{*\beta}} \exp \dfrac{-\beta F(E-E^{0\prime})}{RT}-\dfrac{c_R(0,t)}{c_O^{*(1-\beta)} c_R^{*\beta}} \exp \dfrac{(1-\beta)F(E-E^{0\prime})}{RT} \tag {6}$$

变换形式为

$$\dfrac {i}{i_0}=\dfrac{c_O(0,t)}{c_O^* } \left (\dfrac{c_O^*}{ c_R^*} \right) ^\beta \exp \dfrac{-\beta F(E-E^{0\prime})}{RT}-\dfrac{c_R(0,t)}{ c_R^*} \left (\dfrac{c_O^*}{ c_R^*} \right)^{-(1-\beta)} \exp \dfrac{(1-\beta)F(E-E^{0\prime})}{RT} \tag {7}$$

把方程(4)带入到(7)中，得：

$$\dfrac {i}{i_0}=\dfrac{c_O(0,t)}{c_O^* } \left (\exp \dfrac{ F(E_{eq}-E^{0\prime})}{RT}\right) ^\beta \exp \dfrac{-\beta F(E-E^{0\prime})}{RT}\\ -\dfrac{c_R(0,t)}{ c_R^*} \left (\exp \dfrac{ F(E_{eq}-E^{0\prime})}{RT} \right)^{-(1-\beta)} \exp \dfrac{(1-\beta)F(E-E^{0\prime})}{RT} \tag {8}$$

化简得到

$$i=i_0 \left [\dfrac {c_O(0,t)}{c_O^*} \exp \dfrac{-\beta F(E-E_{eq})}{RT} - \dfrac {c_R(0,t)}{c_R^*} \exp \dfrac{(1-\beta)F(E-E_{eq})}{RT} \right] \tag {9}$$

定义过电位表达式为

$$\eta=E-E_{eq} \tag {10}$$

因此可得：

$$i=i_0 \left [\dfrac {c_O(0,t)}{c_O^*} \exp \dfrac{-\beta F}{RT} \eta- \dfrac {c_R(0,t)}{c_R^*} \exp \dfrac{(1-\beta)F}{RT} \eta \right] \tag {11}$$

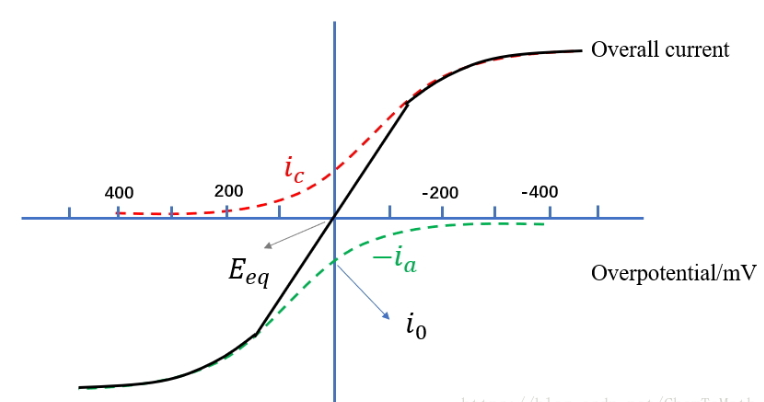
Figure 1. 单步骤单电子氧化还原电对的电流-过电位曲线

从图中可以定性的看出，当过电位越负，总电流几乎和阴极电流$i_c$相近，阳极电流可以忽略；当过电位越正时，总电流几乎和阳极电流$i_a$相近，阴极电流可以忽略。当电位在平衡电位$E_{eq}$附近时，电流变化非常大，这是因为指数项占主导，几乎成指数变化；但是当过电位的绝对值很大的时候，反应速率很大，那么表面的物质浓度就会很小，本体浓度向表面传质速率将会占主导，即使过电位再增加也不能提高电流，因为此时电流(反应速率)已被传质速率控制，所以看到图中的稳定(极限)电流(平线)。

如果不考虑传质的影响。 条件：溶液被充分搅拌，或者电流维持在很小的值，目的是为了让表面浓度surface concentration与本体浓度bulk concentration没有太大差异，保证$\dfrac {c_O(0,t)}{c_O^*}$与$\dfrac {c_R(0,t)}{c_R^*}$的值在0.9-1.1之间， 从(4)可得：

$$i=i_0 \left [ \exp \dfrac{-\beta F}{RT} \eta- \exp \dfrac{(1-\beta)F}{RT} \eta \right] \tag {12}$$

由于不考虑传质的影响，那么交换电流的大小就直接放映了动力学快慢，也就是反应活化能。交换电流越小，活化能越大，越需要大的过电位，才能有电流产生；反之，交换电流越大，活化能越小，则在较小的过电位条件下就可以产生较大的电流。

---

过电位较小时

当过电位$\eta$绝对值比较小的时，$\dfrac{-\beta F}{RT} \eta$比较小，那么根据$e^x=1+x$ (当$x$足够小时）

$$i=i_0 \left [1+\dfrac{-\beta F}{RT} \eta- 1- \dfrac{(1-\beta)F}{RT} \eta \right]=i_0 \dfrac{ F}{RT} \eta\tag {13}$$

过电位较大时，Tafel slope

当过电位很大的时，其中阳极或者阴极电流可以被忽略。比如，当过电位很负时，

$$\exp \dfrac{-\beta F}{RT} \eta \gg \exp \dfrac{(1-\beta)F}{RT} \eta$$

则

$$i=i_0 \exp \dfrac{-\beta F}{RT} \eta \tag {14}$$

两边取自然对数，得：

$$\ln i=\ln i_0 -\dfrac{\beta F}{RT} \eta \tag{15}$$

变换得到：

$$\eta=\dfrac{RT}{\beta F} \ln i_0 -\dfrac{RT}{\beta F} \ln i \tag{16}$$

变换为 log

$$\eta=\dfrac{2.3RT}{\beta F} \log i_0 -\dfrac{2.3RT}{\beta F} \log i \tag{17}$$

注意，当逆向电流贡献小于1%的时候，Tafel 形式是正确的。
也就是

$$\dfrac {\exp \dfrac{-\beta F}{RT} \eta} {\exp \dfrac{(1-\beta)F}{RT} \eta}=\exp \dfrac{F}{RT} \eta \leqslant 0.01$$

即在$25 ^oC$时，过电位的绝对值要大于118 mV($\vert \eta \vert >118 mV$)。若果电极动力学很快，而达到极限电流，那么就观察不到Tafel 关系，此时必须要排除传质的影响。当电极动力学很慢的时候，而且需要较大过电位才反应时，此时可以得到较好的Tafel 关系式。因此Tafel 关系式，是不可逆动力学的标志。

---

Reference

[1] Allen J. Bard, Larry R. Faulkner; Electrochemical methods-Fundamentals and applications.